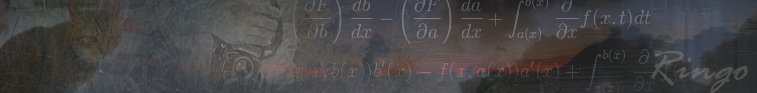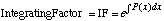開立方根不用計算機

4 的3 次方是4 x 4 x 4 = 64，換言之，64 開3 次方，即64 的立方根便是4，很簡單的。

那66 的立方根是多少？

66 和64 相差不遠，答案必定是 4 再多一點點。

一按計算機，答案是4.0412...

不用計算機，那很難吧？

這裡有個方法：

那一點點，就是數字多出的部分除以3，再除以該數字立方根的平方。

比方說，現在要求66 的立方根，那66 - 64 = 2 就是那多出的部分。所以，立方根多出的部分，就是 2 除以3，再除以64 的立方根的平方，即4的平方，那就是16。而2除3再除16，則等於八分一除3，即0.125除3，約等於0.042。

這多出的一點點再加上原來的4，就是4.042。而4.042 的3 次方，等於66.04，和66相比，誤差只有百分之四左右，不俗吧？

為什麼這方法可以求出立方根？

在微積分裡，

所以

而現在是開立方根，所以設

這就是為何會出現那三分之一。

所以

這方法其實用來求平方根也可以，稍加更改，那一點點超出的部分，就是相差的數目再除以2，然後再除以該數字的平方根。

真‧Advanced Calculus - Woods

《Surely you're joking Mr. Feynman!》一書裡有以下的描述：

『我始終沒有學會的是“圍道積分（contour integration）”。　　

高中物理老師貝德先生給過我一本書，我會的所有積分方法，都是從這本書裏學到的。　　

事情是這樣的：一天下課之後，他叫我留下。“費曼”，他說，“你上課時話太多了，聲音又太大。我知道你覺得這些課太沉悶，現在我給你這本書。以後你坐到後面角落去好好讀這本書，等你全弄懂了之後，我才准你講話。”　　

於是每到上物理課時，不管老師教的是帕斯卡定律或是別的什麼，我都一概不理。我坐在教室的角落，念伍茲（woods）著的這本《高等微積分學》。貝德知道我念過一點《實用微積分》，因此他給我這本真正的大部頭著作——給大學二三年級學生念的教材。書內有傅立葉級數、貝塞爾函數、行列式、橢圓函數——各種我前所未知的奇妙東西。　　

那本書還教你如何對積分符號內的參數求微分。後來我發現，一般大學課程並不怎麼教這個技巧，但我掌握了它的用法，往後還一再地用到它。因此，靠著自修那本書，我做積分的方法往往與眾不同。　　

結果經常發生的是，我在麻省理工或普林斯頓的朋友被某些積分難住，原因卻是他們從學校學來的標準方法不管用。　　

如果那是圍道積分或級數展開，他們都懂得怎麼把答案找出；現在他們卻碰壁了。這時我便使出“積分符號內取微分”的方法——這是因為我有一個與眾不同的工具箱。當其他人用光了他們的工具，還沒法找到解答時，便把問題交給我了！』

正，一定要找這本“Advanced Calculus”出來，看看到底有多利害。

結果，我翻遍了幾間大學的圖書館在線書目，也找它不到。連經常流連的理大拉記，也沒有它的蹤跡。

最後，終於在城大圖書館目錄裡找到它：

Author - Woods, Frederick S. (Frederick Shenstone), 1864-
Title - Advanced calculus : a course arranged with special reference to the needs of students of applied mathematics / by Frederick S. Woods.
Publisher - Boston : Ginn, c1934.
Edition - New ed.

一本古書，而且，無論何時查目錄，都是 always available 的。

雖然找不到 1926 年的第一版，但這本 1934 年版已是夠老的了，應該和第一版相差無幾。

有一天，因工作關係，有機會可進入城大圖書館 ......

順著 QA303.W885 1934 的號碼，在『數學』一欄的書架邊上走，走到幾近窗口的地方，終於見到這本傳說中的奇書。

深啡色的封面，沒有任何設計，只有“Advanced Calculus”和作者名幾個大字，很典型的二三十年代教科書的風格。

伸手慢慢地、慢慢地把它拿出來，幾十年的舊書，生怕一下子不慎，把它弄得甩皮甩骨。

小心地把它輕放在書桌上，輕輕的翻開來，撲鼻的一陣舊書味。正文前的第一頁，用鉛筆寫了幾個英文字。

城大不過二十幾年，70 年代或以前的書理應絕無僅有。正納悶間，細心一看那幾行退了色的鉛筆字：“Donated by Ms Maria, 1934”。

由於沒有太多時間，惟有只翻到“Differentiation under the integral sign”那一章，看個飽。

雖然跑到城大之前，早已在維基百科上看過這個 topic，但看真書的時候，還是有種不可言喻的滿足感，就像看到大師的真跡似的。

不要小看這本古董書，在網上買二手，最平的賣價也要港幣七百多元！

如此拆解微分方程式 ── 精彩！

剛剛在 Youtube 上看到有人放了一條短片，10 分鐘左右，是一個 mini lecture，教大家用一個很基本的想法，便可拆解一條一階線性微分方程式。可貴之處，是每一個步驟也講得很清楚，而且不難，即使只有高中的數學程度也可看得明白。

真的不難理解，而且很快可以看完，去片 ──！






一般坊間數學書的教法，通常是叫你先找出『積分因子』(integrating factor)。假設要解的方程是：


首先將它寫成有 P 和 Q (皆為 x 的函數)：


然後，那個 integrating factor 便自然而然的生了出來：

最後，答案 (即 y) 便是：


這個方法的好處，是過程很機械式，即使你完全不明白，也可以照版煮碗，把答案炮製出來。但就是這種方式令人感到微積分莫測高深，很神秘，心裡有種不舒服的感覺。

而片中的 mini lecture 用了 5 分鐘左右去解釋一些基本的東西，例如 equating coefficients 可知 an = bn，e 函數的定義等等。

餘下的 5 分鐘左右就 step by step 教你如何拆解。

簡單、清楚、易明。精彩！

沈詩鈞學啲乜？

圖片來源：星島日報

神童入浸大，上完一堂數學課，隨即在記者面前大嘆課程太淺，一臉滿不在乎的樣子。


當記者問他學了些甚麼，詩鈞即回應道：「你梗係唔明啦」；面對記者的再三追問，他指「你都唔知（數學名詞）係乜名。」(9月5日星島日報)

我在電視面前看著，覺得此 9 歲人仔，天才得黎，真係有啲寸。之後不知是哪一個電視台，搵到料，知道神童在那堂『數學分析』學過什麼，隨即在電視畫面上讓好奇的觀眾看個飽：

記得那把 voice over 的聲音還說：『可能你同我都未必會明 ......』

也難怪阿神童話個記者：『你梗係唔明啦！』

但由於我最討厭人懶神秘，又對電視台如此『講啲又唔講啲』的報導手法甚為不滿，姑且在此說明一下。

其實，又不至於一字咁淺，但擁有基礎數學常識的人，都不難看得明，上式只是想說明一個集合 “A”裡面有什麼而已。所謂集 (set)，簡單來說就只是一堆個別物件的集合而已。雖然 Set Theory 在數學裡是一個大分支，亦可以玩到好大、好深奧，但要明白其基本定義，也並非常人遙不可及的事。

『A 是一個集，裡面包含的東西叫 x，所有這些 x 都必須乎合一個條件，就是 x 的平方加 3 乘以 x 再加 1 等於零。』

就是如此。

但偏偏數學家就喜歡將一句說話用超濃縮的方式，再以數學符號演繹一次，一般人都會望而卻步。但數學架構要嚴謹，就必須如此。

9 歲就擁有預科數學程度的阿沈，難怪可以在眾記者面前『大你一大』。可惜一眾網民卻不受這一套，在 Yahoo 新聞網頁上留言大罵。網民 jasonxfeng 如此評論神童鈞：

『我系電視新聞看到佢接受記者的訪問,佢雖然讀書勁,但又自大,又串.令到我對佢好反感!
太冇禮貌啦~!
佢仲系小朋友,以后都吾知點算?
要努力學習禮貌吖~!』

但亦有網民撐佢，ivjo23 說：

『咩大家9 years old時就好大體, 好polite, 好識幾時講啱聽既說話? 莫講9 years old, 19 years old 都好多好多幼稚既人啦, 大家又駛咩咁嬲? 小朋友慢慢教咪得lor, 比個小朋友激親, 你又有幾成熟呢? 』

個人認為，9 歲識幾多大體，幾多謙虛？神童鈞如此表現，沈父責無旁貸。

也許鈞仔有天閒來無事，在浸大圖書館裡流連時，偶爾翻開陳省身和丘成桐的數學論文時，才知天外有天。

除了數學，佢重有大把嘢要學！